STA 506 2.0 Linear Regression Analysis
Lecture 2-3: Simple Linear Regression
Dr Thiyanga S. Talagala
2020-09-05
Recap: correlation
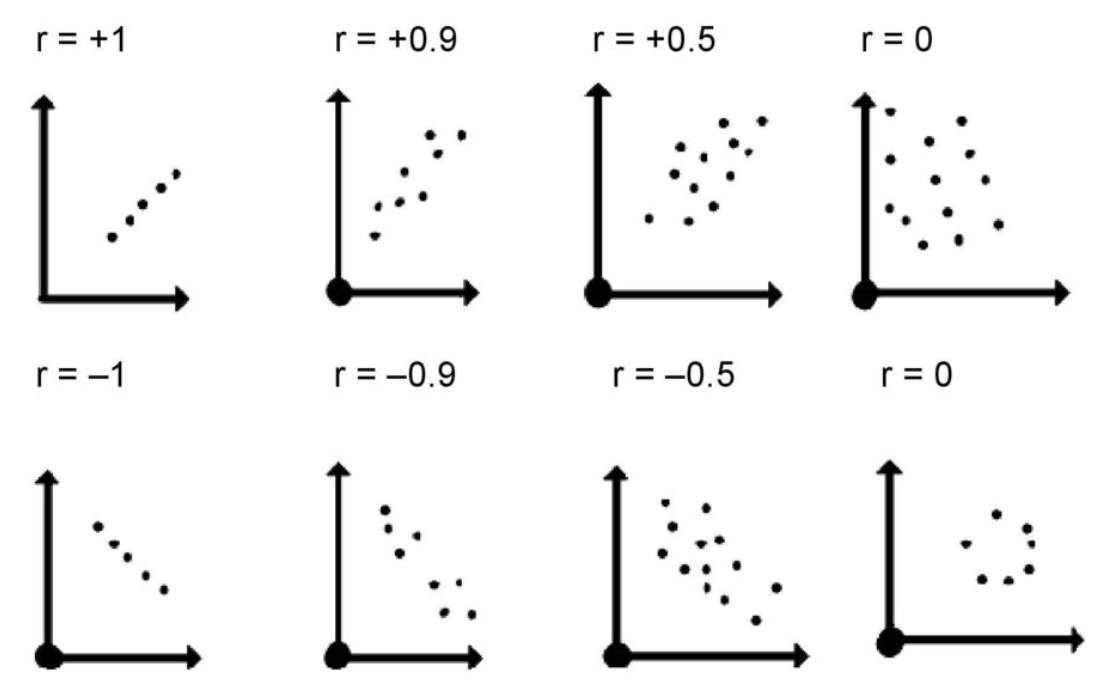
Recap: correlation (cont.)

| value | interpretation |
|---|---|
| -1 | Perfect negative |
| (-1, -0.75) | Strong negative |
| (-0.75, -0.5) | Moderate negative |
| (-0.5, -0.25) | Weak negative |
| (-0.25, 0.25) | No linear association |
| (0.25, 0.5) | Weak positive |
| (0.5, 0.75) | Moderate positive |
| (0.75, 1) | Strong positive |
| 1 | Perfect positive |
Recap: Terminologies
Response variable: dependent variable
Explanatory variables: independent variables, predictors, regressor variables, features (in Machine Learning)
Response variable = Model function + Random Error
Parameter
Statistic
Estimator
Estimate
In-class
In-class
Simple Linear Regression
Simple - single regressor
Linear - has a dual role here.
It may be taken to describe the fact that the relationship between YY and XX is linear. The word linear refers to the fact that the regression parameters enter in a linear fashion.
Meaning of Linear Model
| What about this?
Y=β0+β1x1+β2x2+ϵY=β0+β1x1+β2x2+ϵ
Meaning of Linear Model
| What about this?
Y=β0+β1x1+β2x2+ϵY=β0+β1x1+β2x2+ϵ
| Linear or nonlinear?
Y=β0+β1x+β2x2+ϵY=β0+β1x+β2x2+ϵ
Meaning of Linear Model
| What about this?
Y=β0+β1x1+β2x2+ϵY=β0+β1x1+β2x2+ϵ
| Linear or nonlinear?
Y=β0+β1x+β2x2+ϵY=β0+β1x+β2x2+ϵ | Linear or nonlinear?
Y=β0eβ1x+ϵY=β0eβ1x+ϵ
Meaning of Linear Model
| What about this?
Y=β0+β1x1+β2x2+ϵY=β0+β1x1+β2x2+ϵ
| Linear or nonlinear?
Y=β0+β1x+β2x2+ϵY=β0+β1x+β2x2+ϵ | Linear or nonlinear?
Y=β0eβ1x+ϵY=β0eβ1x+ϵ
What about this?
Y=αXβ1Xγ2Xδ3+ϵY=αXβ1Xγ2Xδ3+ϵ
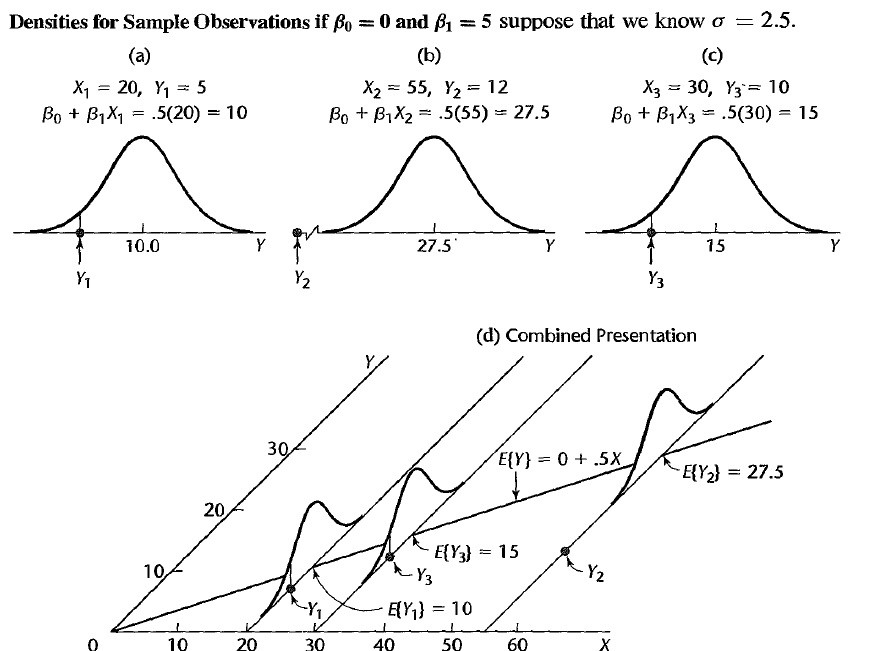
True relationship between X and Y in the population
Y=f(X)+ϵY=f(X)+ϵ
If ff is approximated by a linear function
Y=β0+β1X+ϵY=β0+β1X+ϵ
The error terms are normally distributed with mean 00 and variance σ2σ2. Then the mean response, YY, at any value of the XX is
E(Y|X=xi)=E(β0+β1xi+ϵ)=β0+β1xiE(Y|X=xi)=E(β0+β1xi+ϵ)=β0+β1xi
For a single unit (yi,xi)(yi,xi)
yi=β0+β1xi+ϵi where ϵi∼N(0,σ2)yi=β0+β1xi+ϵi where ϵi∼N(0,σ2)
We use sample values (yi,xi)(yi,xi) where i=1,2,...ni=1,2,...n to estimate β0β0 and β1β1.
The fitted regression model is
^Yi=ˆβ0+ˆβ1xi^Yi=^β0+^β1xi
Normal distribution
[1] 5.008403
[1] 5.082935Normal distribution
Normal distribution
From: https://towardsdatascience.com/do-my-data-follow-a-normal-distribution-fb411ae7d832
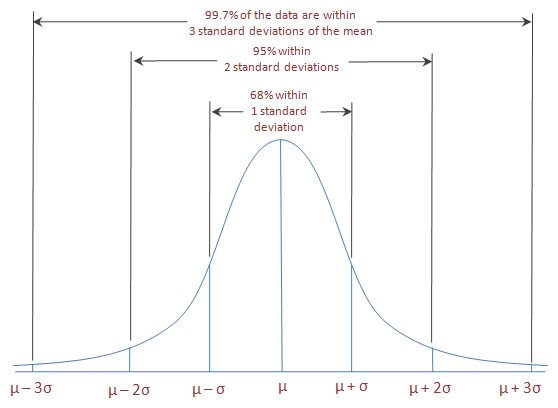
Normal distribution

From: https://towardsdatascience.com/do-my-data-follow-a-normal-distribution-fb411ae7d832
Normal distribution
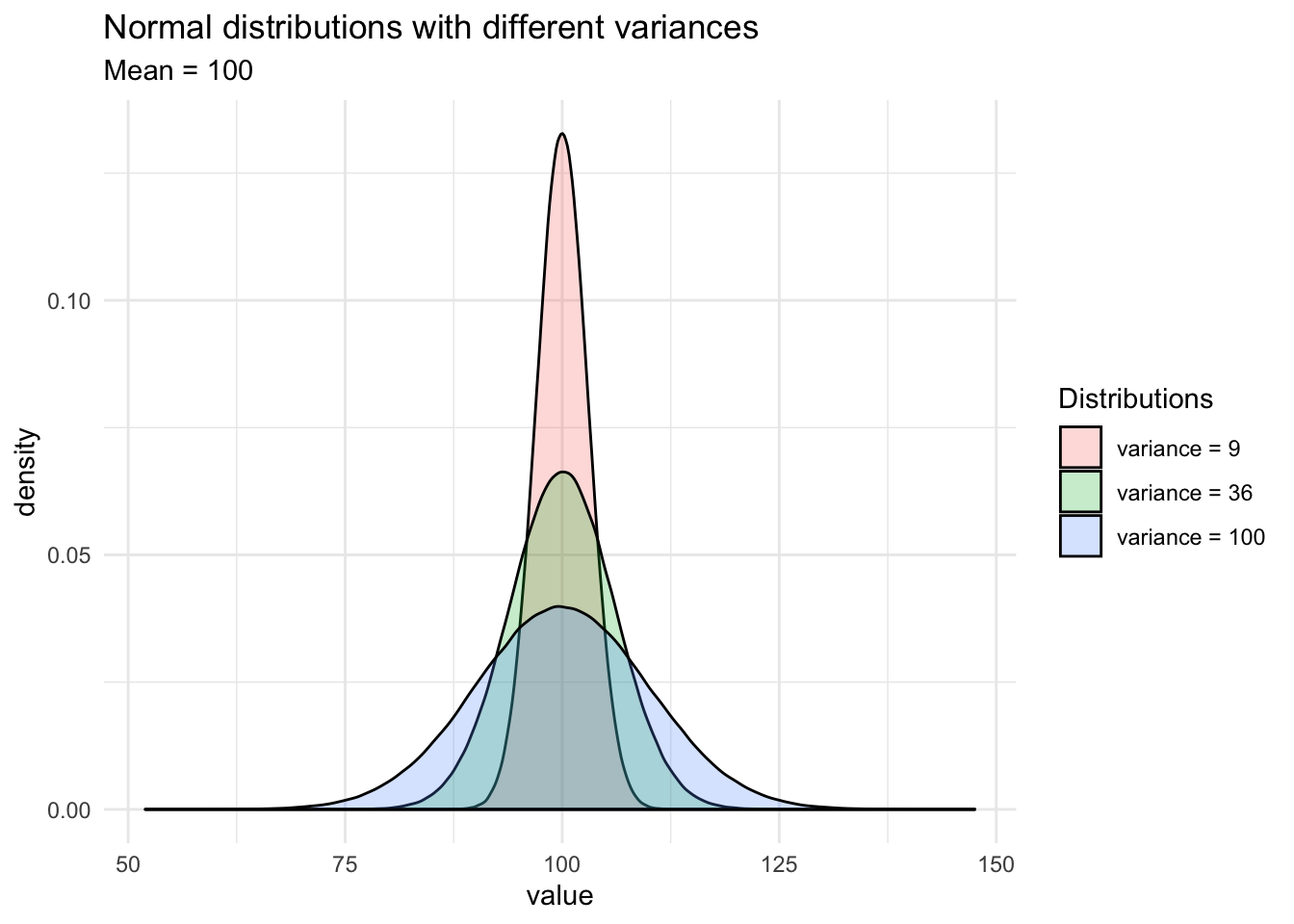
From: https://towardsdatascience.com/do-my-data-follow-a-normal-distribution-fb411ae7d832
Buckle up!
Let's walk through the steps.
In-class
True relationship between X and Y in the population
Y=f(X)+ϵY=f(X)+ϵ
In-class
True relationship between X and Y in the population
Y=f(X)+ϵY=f(X)+ϵ
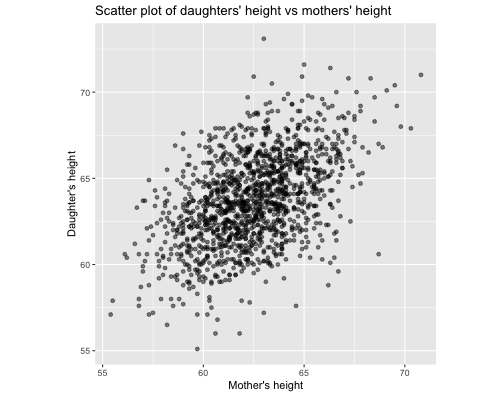
Example: Suppose you want to model daughters' height as a function of mothers' height.
Do you think an exact (deterministic) relationship exists between these two variables?
In-class
True relationship between X and Y in the population
Y=f(X)+ϵY=f(X)+ϵ
Example: Suppose you want to model daughters' height as a function of mothers' height.
Do you think an exact (deterministic) relationship exists between these two variables?
Why?
In-class
True relationship between X and Y in the population
Y=f(X)+ϵY=f(X)+ϵ
Example: Suppose you want to model daughters' height as a function of mothers' height.
Do you think an exact (deterministic) relationship exists between these two variables?
- Daughters' height may depend on many other variables than Mothers' height.
In-class
True relationship between X and Y in the population
Y=f(X)+ϵY=f(X)+ϵ
Example: Suppose you want to model daughters' height as a function of mothers' height.
Do you think an exact (deterministic) relationship exists between these two variables?
Daughters' height may depend on many other variables than Mothers' height.
Even if many variables are included in the model, it is unlikely that we can predict the daughter's height exactly. Why?
In-class
True relationship between X and Y in the population
Y=f(X)+ϵY=f(X)+ϵ
Example: Suppose you want to model daughters' height as a function of mothers' height.
Do you think an exact (deterministic) relationship exists between these two variables?
Daughters' height may depend on many other variables than Mothers' height.
Even if many variables are included in the model, it is unlikely that we can predict the daughter's height exactly. Why?
There will almost certainly be some variations in the model predictions that cannot be modelled, or explained.
These unexplained variances are assumed to be caused by the unexplainable random phenomena, so they can be referred to as random error.
In-class
In-class: Population Regression Line
True relationship between X and Y in the population
Y=f(X)+ϵY=f(X)+ϵ
If ff is approximated by a linear function
Y=β0+β1X+ϵY=β0+β1X+ϵ
The error terms are normally distributed with mean 00 and variance σ2σ2. Then the mean response, YY, at any value of the XX is
E(Y|X=xi)=E(β0+β1xi+ϵ)=β0+β1xiE(Y|X=xi)=E(β0+β1xi+ϵ)=β0+β1xi
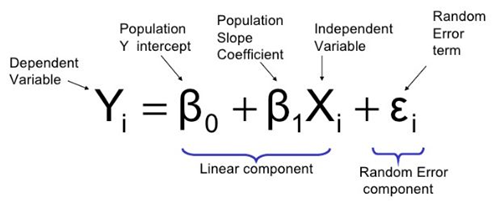
In-class: Population Regression Line
E(Y|X=xi)=E(β0+β1xi+ϵ)=β0+β1xiE(Y|X=xi)=E(β0+β1xi+ϵ)=β0+β1xi
For a single unit (yi,xi)(yi,xi)
yi=β0+β1xi+ϵi where ϵi∼N(0,σ2)yi=β0+β1xi+ϵi where ϵi∼N(0,σ2)
Take a sample:
The fitted regression line is
^Yi=ˆβ0+ˆβ1xi^Yi=^β0+^β1xi
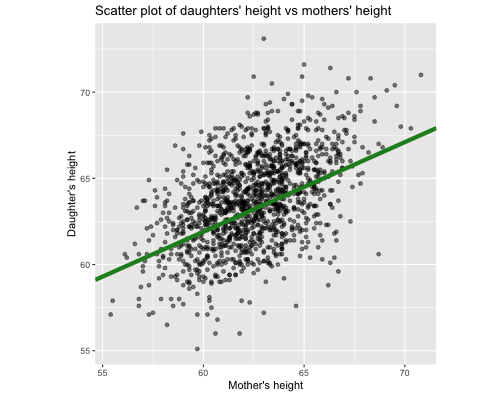
Our example (0.52, 30.7)
Dashboard: https://statisticsmart.shinyapps.io/SimpleLinearRegression/
Our example (0.582, 28.5)
Dashboard: https://statisticsmart.shinyapps.io/SimpleLinearRegression/
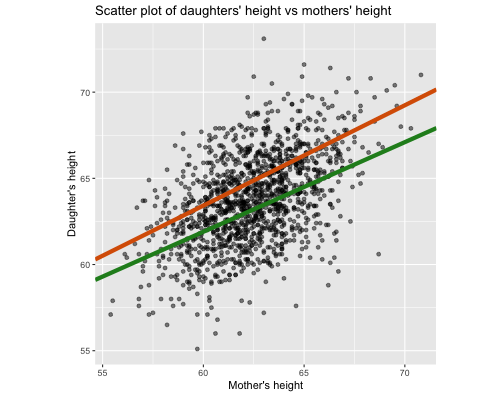
Our example (0.5, 32.5)
Dashboard: https://statisticsmart.shinyapps.io/SimpleLinearRegression/
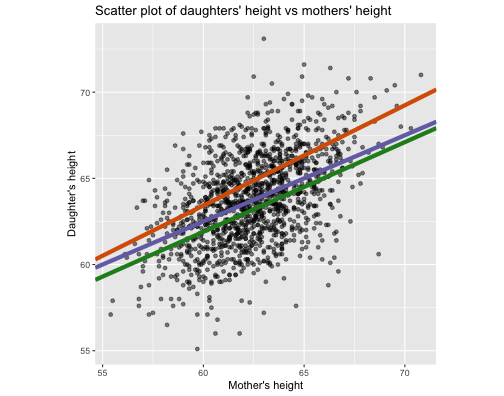
Which is the best?
Which is the best?
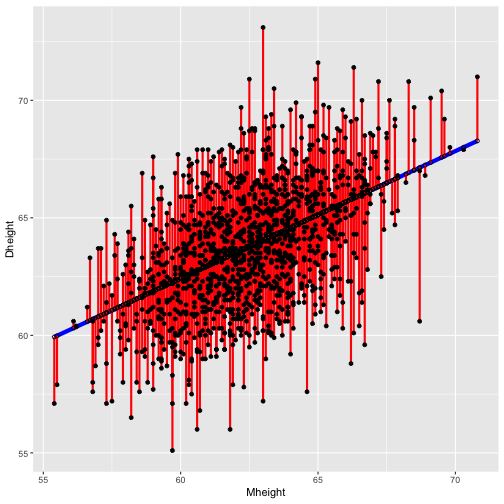
Sum of squares of Residuals
SSR=e21+e22+...+e2nSSR=e21+e22+...+e2n
Evaluating your answers: Fitted values
Dheight = 30.7 + 0.52Mheight
df <- alr3::heightsdf$fitted <- 30.7 + (0.52*df$M)head(df,10) Mheight Dheight fitted1 59.7 55.1 61.7442 58.2 56.5 60.9643 60.6 56.0 62.2124 60.7 56.8 62.2645 61.8 56.0 62.8366 55.5 57.9 59.5607 55.4 57.1 59.5088 56.8 57.6 60.2369 57.5 57.2 60.60010 57.3 57.1 60.496First fitted value: 30.7 + (0.52 * 59.7) = 61.744
Evaluating your answers
Sum of squares of Residuals
SSR=e21+e22+...+e2nSSR=e21+e22+...+e2n
Dheight = 30.7 + 0.52Mheight
Mheight Dheight fitted resid_squared1 59.7 55.1 61.744 44.1427362 58.2 56.5 60.964 19.9272963 60.6 56.0 62.212 38.5889444 60.7 56.8 62.264 29.8552965 61.8 56.0 62.836 46.7308966 55.5 57.9 59.560 2.7556007 55.4 57.1 59.508 5.7984648 56.8 57.6 60.236 6.9484969 57.5 57.2 60.600 11.56000010 57.3 57.1 60.496 11.532816[1] 7511.118SSR: 7511.118
Evaluating your answers
Dashboard: https://statisticsmart.shinyapps.io/SimpleLinearRegression/

Green: 7511.118 (0.52, 30.7)
Orange: 8717.41 (0.582, 28.5)
Purple: 7066.075 (0.5, 32.5)
How to estimate β0β0 and β1β1?
Sum of squares of Residuals
SSR=e21+e22+...+e2nSSR=e21+e22+...+e2n
Observed value
yiyi
Fitted value
^Yi^Yi
^Yi=ˆβ0+ˆβ1xi^Yi=^β0+^β1xi
Residual
ei=yi−^Yiei=yi−^Yi
The least-squares regression approach chooses coefficients ˆβ0^β0 and ˆβ1^β1 to minimize SSRSSR.
Least-squares Estimation of the Parameters
yi=β0+β1xi+ϵi, i =1, 2, 3, ...n .yi=β0+β1xi+ϵi, i =1, 2, 3, ...n .
The least squares criterion is
S(β0,β1)=n∑i=1(yi−β0−β1xi)2.S(β0,β1)=n∑i=1(yi−β0−β1xi)2.
Least-squares Estimation of the Parameters (cont.)
The least squares criterion is
S(β0,β1)=n∑i=1(yi−β0−β1xi)2.S(β0,β1)=n∑i=1(yi−β0−β1xi)2.
The least-squares estimators of β0β0 and β1β1, say ^β0^β0 and ^β1,^β1, must satisfy
∂S∂β0|^β0,^β1=−2n∑i=1(yi−^β0−^β1xi)=0∂S∂β0|^β0,^β1=−2n∑i=1(yi−^β0−^β1xi)=0
and
∂S∂β1|^β0,^β1=−2n∑i=1(yi−^β0−^β1xi)xi=0.∂S∂β1|^β0,^β1=−2n∑i=1(yi−^β0−^β1xi)xi=0.
Least-squares Estimation of the Parameters (cont.)
Simplifying the two equations yields
n^β0+^β1n∑i=1xi=n∑i=1yi,n^β0+^β1n∑i=1xi=n∑i=1yi, ^β0n∑i=1xi+^β1n∑i=1x2i=n∑i=1yixi.
These are called least-squares normal equations.
Least-squares Estimation of the Parameters (cont.)
n^β0+^β1n∑i=1xi=n∑i=1yi,
^β0n∑i=1xi+^β1n∑i=1x2i=n∑i=1yixi.
The solution to the normal equation is
^β0=ˉy−^β1ˉx,
and
^β1=∑ni=1yixi−∑ni=1yi∑ni=1xin∑ni=1x2i−(∑ni=1xi)2n.
The fitted simple linear regression model is then
ˆY=^β0+ˆβ1x
Least-squares fit
Try this with R
library(alr3) # to load the datasetmodel1 <- lm(Dheight ~ Mheight, data=heights)model1Call:lm(formula = Dheight ~ Mheight, data = heights)Coefficients:(Intercept) Mheight 29.9174 0.5417Least-squares fit and your guesses
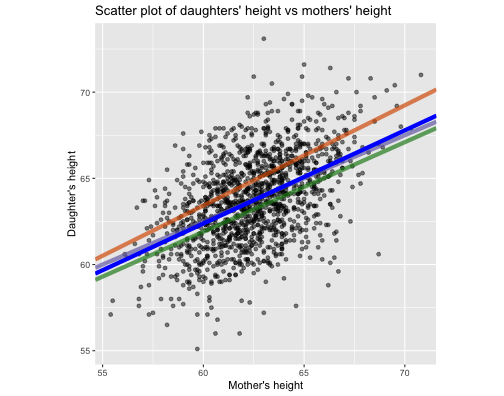
fit <- 0.5417 * df$Mheight + 29.9174sum((df$Dheight - fit)^2)[1] 7051.97Least square fit and your guesses
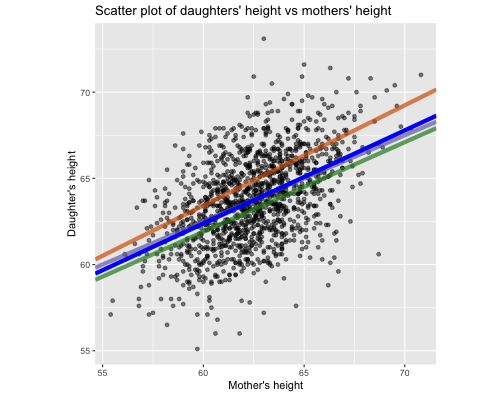
Green: 7511.118 (0.52, 30.7)
Orange: 8717.41 (0.582, 28.5)
Purple: 7066.075 (0.5, 32.5)
Blue: 7051.97 (0.541, 29.9174)
Try this with R
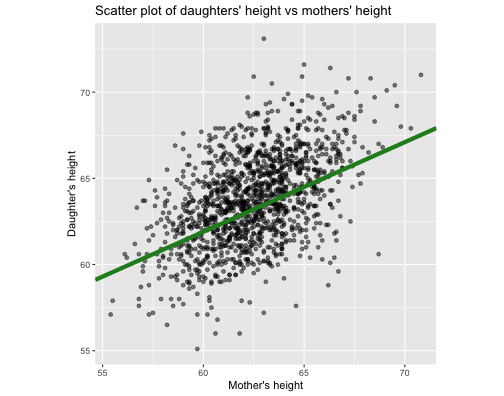
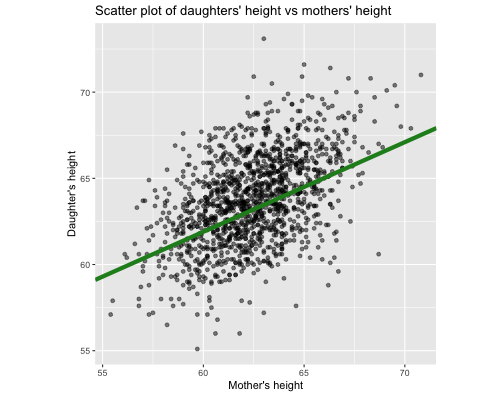
library(alr3) # to load the datasetmodel1 <- lm(Dheight ~ Mheight, data=heights)model1summary(model1)Call:lm(formula = Dheight ~ Mheight, data = heights)Residuals: Min 1Q Median 3Q Max -7.397 -1.529 0.036 1.492 9.053 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 29.91744 1.62247 18.44 <2e-16 ***Mheight 0.54175 0.02596 20.87 <2e-16 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 2.266 on 1373 degrees of freedomMultiple R-squared: 0.2408, Adjusted R-squared: 0.2402 F-statistic: 435.5 on 1 and 1373 DF, p-value: < 2.2e-16Visualise the model: Try with R
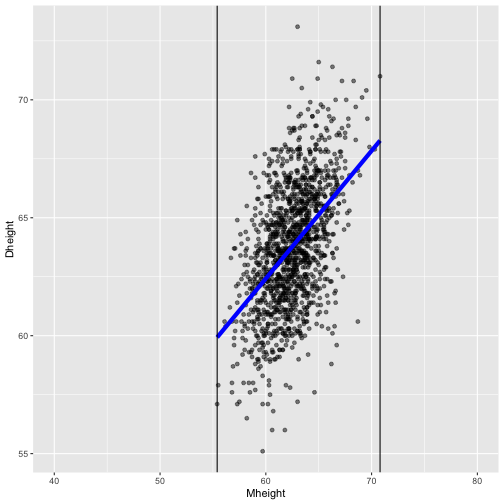
ggplot(data=heights, aes(x=Mheight, y=Dheight)) + geom_point(alpha=0.5) + geom_smooth(method="lm", se=FALSE, col="blue", lwd=2) + theme(aspect.ratio = 1)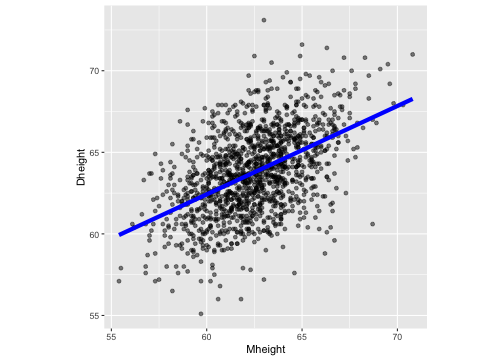
Least squares regression line
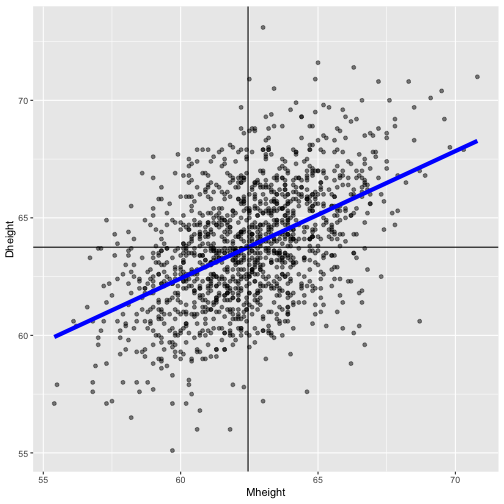
summary(alr3::heights) Mheight Dheight Min. :55.40 Min. :55.10 1st Qu.:60.80 1st Qu.:62.00 Median :62.40 Median :63.60 Mean :62.45 Mean :63.75 3rd Qu.:63.90 3rd Qu.:65.60 Max. :70.80 Max. :73.10The LSRL passes through the point ( ˉx, ˉy), that is (sample mean of x, sample mean of y)
Least squares regression line
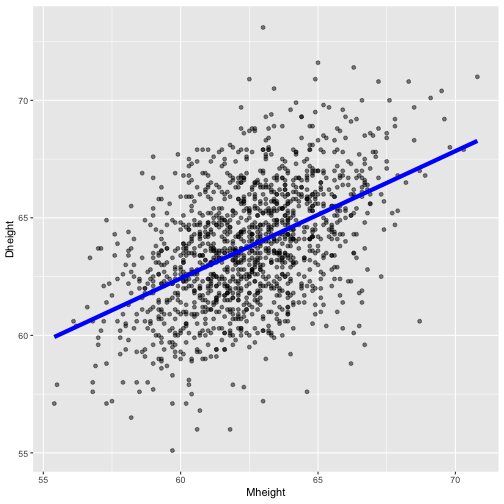
The least squares regression line doesn't match the population regression line perfectly, but it is a pretty good estimate. And, of course, we'd get a different least squares regression line if we took another (different) sample.
Extrapolation: beyond the scope of the model.
Next Lecture
More work - Simple Linear Regression, Residual Analysis, Predictions