Steps
Fit a model.
Visualize the fitted model.
Model Adequacy Checking
Interpret the coefficients.
Make predictions using the fitted model.
Fitted model
library(alr4) # to load the datasetLoading required package: carLoading required package: carDataLoading required package: effectslattice theme set by effectsTheme()See ?effectsTheme for details.model1 <- lm(dheight ~ mheight, data=Heights)model1Call:lm(formula = dheight ~ mheight, data = Heights)Coefficients:(Intercept) mheight 29.9174 0.5417Model summary
summary(model1)Call:lm(formula = dheight ~ mheight, data = Heights)Residuals: Min 1Q Median 3Q Max -7.397 -1.529 0.036 1.492 9.053 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 29.91744 1.62247 18.44 <2e-16 ***mheight 0.54175 0.02596 20.87 <2e-16 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 2.266 on 1373 degrees of freedomMultiple R-squared: 0.2408, Adjusted R-squared: 0.2402 F-statistic: 435.5 on 1 and 1373 DF, p-value: < 2.2e-16Interesting questions come to mind
How well does this equation fit the data?
Is the model likely to be useful as a predictor?
Are any of the basic assumptions violated, and if so, how series is this?
All of these questions must be investigated before using the model.
Residuals play a key role in answering the questions.
Model assumptions
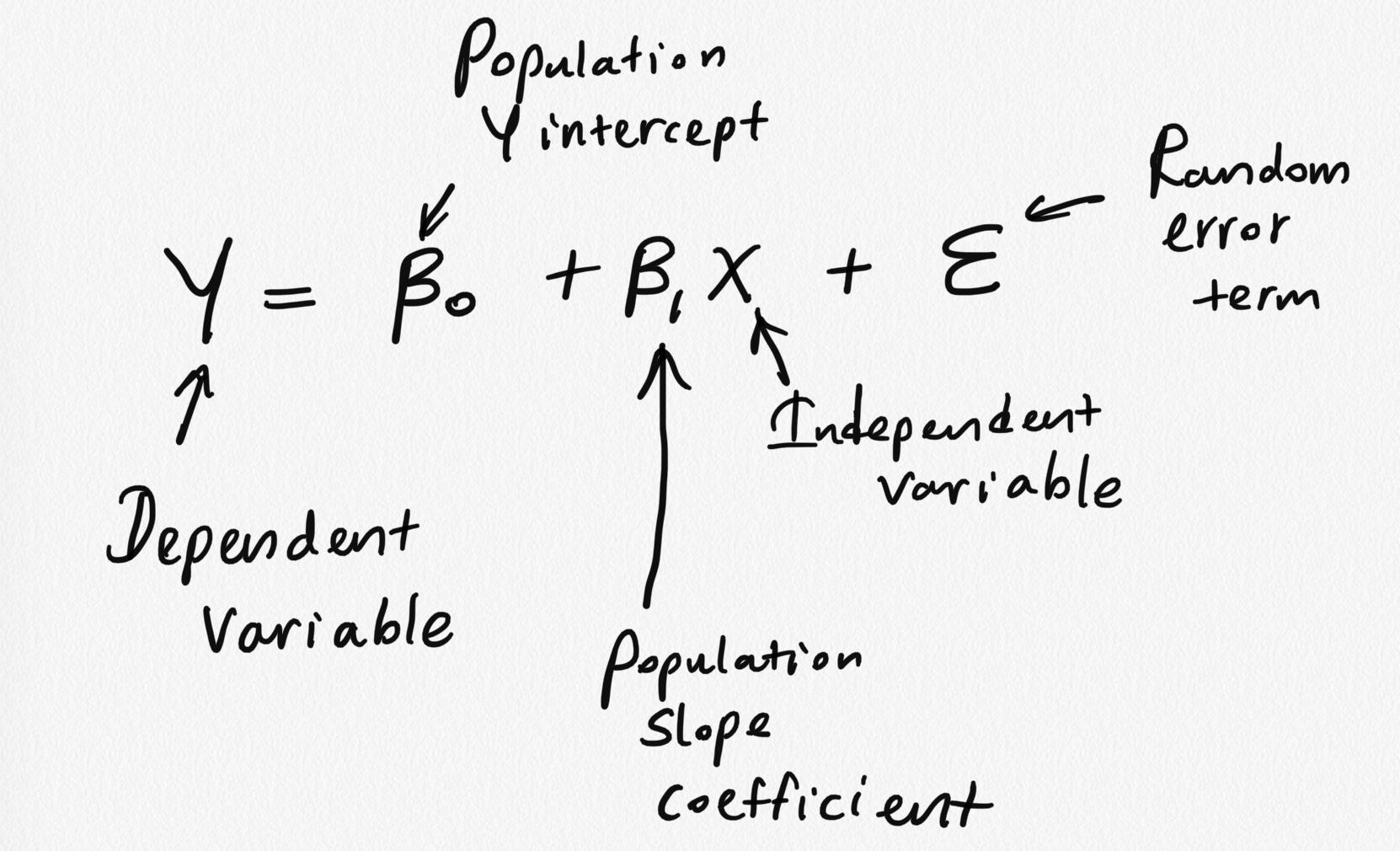
1) The mean of the response, E(Yi), at each value of the predictor, xi, is a Linear function of the xi
Model assumptions
2) The error term ϵ has zero mean.
3) At each value of the predictor, x, errors have equal, constant variance σ2.
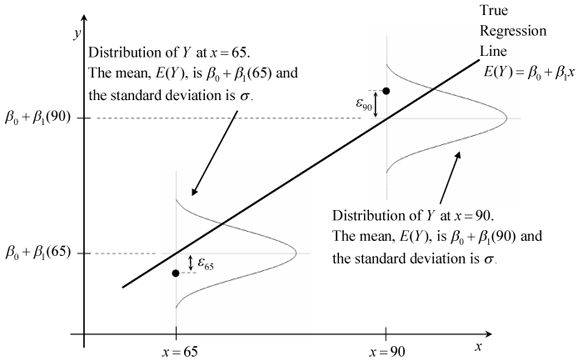
source: http://reliawiki.org/index.php/Simple_Linear_Regression_Analysis
Model assumptions
4) The error are uncorrelated.
5) At each value of the predictor, x the errors are normally distributed
Taking together 4 and 5 imply the errors are independent random variables.
Assumption 5 is required for parametric statistical inference (Hypothesis testing, Interval estimation).
An alternative way to describe all four (2-5) assumptions is that the errors, ϵi, are independent normal random variables with mean zero and constant variance, σ2.
Diagnosing violations of the assumptions
Diagnosing methods are primarily based on model residuals.
Residuals
ei=Observed value−Fitted value
ei=yi−^Yi
- Deviation between the observed value (true value) and fitted value.
df <- alr4::Heightsdf$fitted <- 30.7 + (0.52*df$mheight)head(df,10) mheight dheight fitted1 59.7 55.1 61.7442 58.2 56.5 60.9643 60.6 56.0 62.2124 60.7 56.8 62.2645 61.8 56.0 62.8366 55.5 57.9 59.5607 55.4 57.1 59.5088 56.8 57.6 60.2369 57.5 57.2 60.60010 57.3 57.1 60.496First fitted value: 30.7 + (0.52 * 59.7) = 61.744
df <- alr4::Heightsdf$fitted <- 30.7 + (0.52*df$mheight)df$residuals <- df$dheight - df$fittedhead(df,10) mheight dheight fitted residuals1 59.7 55.1 61.744 -6.6442 58.2 56.5 60.964 -4.4643 60.6 56.0 62.212 -6.2124 60.7 56.8 62.264 -5.4645 61.8 56.0 62.836 -6.8366 55.5 57.9 59.560 -1.6607 55.4 57.1 59.508 -2.4088 56.8 57.6 60.236 -2.6369 57.5 57.2 60.600 -3.40010 57.3 57.1 60.496 -3.396First fitted value: 30.7 + (0.52 * 59.7) = 61.744
First residual value: 55.1 - 61.744 = -6.644
It is convenient to think of residuals as the realized or observed values of the model error.
Residuals have zero mean.
Residuals are not independent.
Observation-level statistics: augment()
library(broom)library(tidyverse)model1_fitresid <- augment(model1)model1_fitresid# A tibble: 1,375 × 8 dheight mheight .fitted .resid .hat .sigma .cooksd .std.resid <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 55.1 59.7 62.3 -7.16 0.00172 2.26 0.00862 -3.16 2 56.5 58.2 61.4 -4.95 0.00310 2.26 0.00743 -2.19 3 56 60.6 62.7 -6.75 0.00118 2.26 0.00523 -2.98 4 56.8 60.7 62.8 -6.00 0.00113 2.26 0.00397 -2.65 5 56 61.8 63.4 -7.40 0.000783 2.26 0.00418 -3.27 6 57.9 55.5 60.0 -2.08 0.00707 2.27 0.00303 -0.923 7 57.1 55.4 59.9 -2.83 0.00725 2.27 0.00574 -1.25 8 57.6 56.8 60.7 -3.09 0.00492 2.27 0.00461 -1.37 9 57.2 57.5 61.1 -3.87 0.00395 2.26 0.00579 -1.71 10 57.1 57.3 61.0 -3.86 0.00421 2.26 0.00616 -1.71 # … with 1,365 more rowsResidual analysis
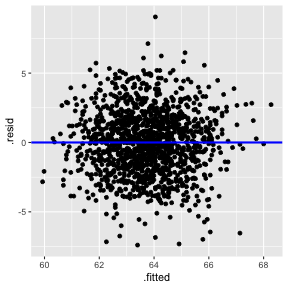
Plot of residuals vs fitted values
This is useful for detecting several common types of model inadequacies.
Our example
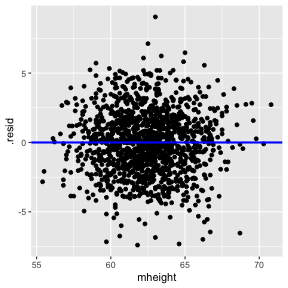
1) The relationship between the response Y and the regressors is linear, at least approximately. (Residuals vs Fitted/ Residual vs X - this is optional in Simple Linear Regression)
2) The error term ϵ has zero mean. (Residuals vs Fitted)
3) The error term ϵ has constant variance σ2. (Residuals vs Fitted)
Residuals vs Fitted
Residuals vs X
Note
In simple linear regression, it is not necessary to plot residuals versus both fitted values and regressor variable. The reason is fitted values are linear combinations of the regressor variable, so the plot would only differ in the scale for the abscissa.
4) The error are uncorrelated.
- Often, we can conclude that the this assumption is sufficiently met based on a description of the data and how it was collected.
Use a random sample to ensure independence of observations.
- If the time sequence in which the data were collected is known, plot of residuals in time sequence.
5) The errors are normally distributed.
ggplot(model1_fitresid, aes(x=.resid))+ geom_histogram(colour="white")+ggtitle("Distribution of Residuals")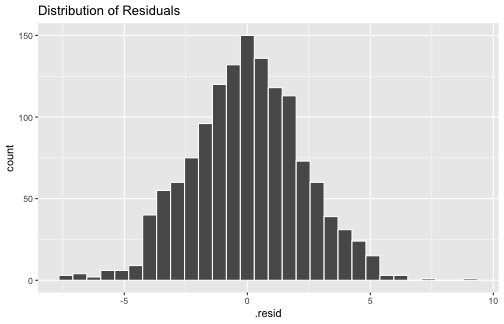
ggplot(model1_fitresid, aes(sample=.resid))+ stat_qq() + stat_qq_line()+labs(x="Theoretical Quantiles", y="Sample Quantiles")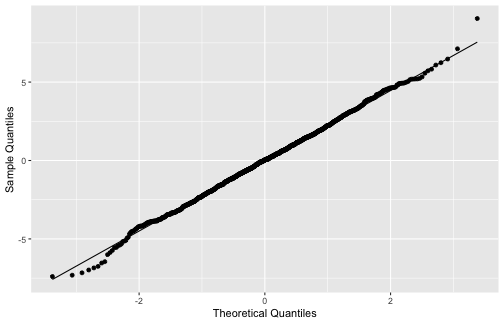
shapiro.test(model1_fitresid$.resid) Shapiro-Wilk normality testdata: model1_fitresid$.residW = 0.99859, p-value = 0.33345) The errors are normally distributed (cont.)
H0: Errors are normally distributed.
H1: Errors are not normally distributed.
Coefficient of Determination
Residuals measure the variability in the response variable not explained by the regression model.
Coefficient of Determination
R2=SSMSST=1−SSRSST
SST - A measure of the variability in y without considering the effect of the regressor variable x.
Measures the variation of y values around their mean.
SSM - Explained variation attributable to factors other than the relationship between x and y.
Notation: SSR or SSE - A measure of the variability in y remaining after x has been considered.
R2 - Proportion of variation in Y explained by the relation relationship of Y with x.
Coefficient of Determination
0≤R2≤1.
Values of R2 that are close to 1 imply that most of the variability in Y is explained by the regression model.
R2 should be interpreted with caution. (We will talk more on this in multiple linear regression analysis)
Our example
summary(model1)Call:lm(formula = dheight ~ mheight, data = Heights)Residuals: Min 1Q Median 3Q Max -7.397 -1.529 0.036 1.492 9.053 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 29.91744 1.62247 18.44 <2e-16 ***mheight 0.54175 0.02596 20.87 <2e-16 ***---Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Residual standard error: 2.266 on 1373 degrees of freedomMultiple R-squared: 0.2408, Adjusted R-squared: 0.2402 F-statistic: 435.5 on 1 and 1373 DF, p-value: < 2.2e-1624% of the variability in daughter's height is accounted by the regression model.
R2 = 24.08%
Maybe you have one or more omitted variables. It is important to consider other factors that might influence the daughter's height:
Father's height
Physical activities performed by the daughter
Food nutrition, etc.
Maybe the functional form of the regression form is incorrect (so you have to add some quadratic, or cubic terms...). At the same time a transformation can be an alternative (if appropriate).
Maybe could be the effect of a group of outlier (maybe not one...).
A large R2 does not necessarily imply that the regression model will be an accurate predictor.
R2 does not measure the appropriateness of the linear model.
R2 will often large even though Y and X are nonlinearly related.
Relationship between r and R2
cor(Heights$mheight, Heights$dheight)[1] 0.4907094cor(Heights$mheight, Heights$dheight)^2[1] 0.2407957Is correlation enough?
Correlation is only a measure of association and is of little use in prediction.
Regression analysis is useful in developing a functional relationship between variables, which can be used for prediction and making inferences.
Next Lecture
More work - Simple Linear Regression, Hypothesis testing, Predictions
Acknowledgement
Introduction to Linear Regression Analysis, Douglas C. Montgomery, Elizabeth A. Peck, G. Geoffrey Vining
All rights reserved by