What does a statistician do?
What does a statistician do?
# A tibble: 15 × 6 country continent year lifeExp pop gdpPercap <fct> <fct> <int> <dbl> <int> <dbl> 1 Afghanistan Asia 1952 28.8 8425333 779. 2 Afghanistan Asia 1957 30.3 9240934 821. 3 Afghanistan Asia 1962 32.0 10267083 853. 4 Afghanistan Asia 1967 34.0 11537966 836. 5 Afghanistan Asia 1972 36.1 13079460 740. 6 Afghanistan Asia 1977 38.4 14880372 786. 7 Afghanistan Asia 1982 39.9 12881816 978. 8 Afghanistan Asia 1987 40.8 13867957 852. 9 Afghanistan Asia 1992 41.7 16317921 649.10 Afghanistan Asia 1997 41.8 22227415 635.11 Afghanistan Asia 2002 42.1 25268405 727.12 Afghanistan Asia 2007 43.8 31889923 975.13 Albania Europe 1952 55.2 1282697 1601.14 Albania Europe 1957 59.3 1476505 1942.15 Albania Europe 1962 64.8 1728137 2313.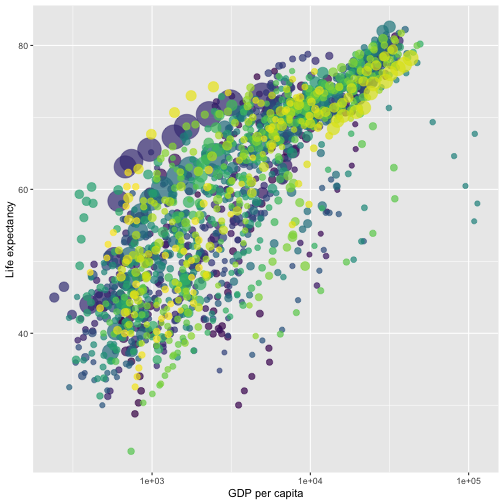
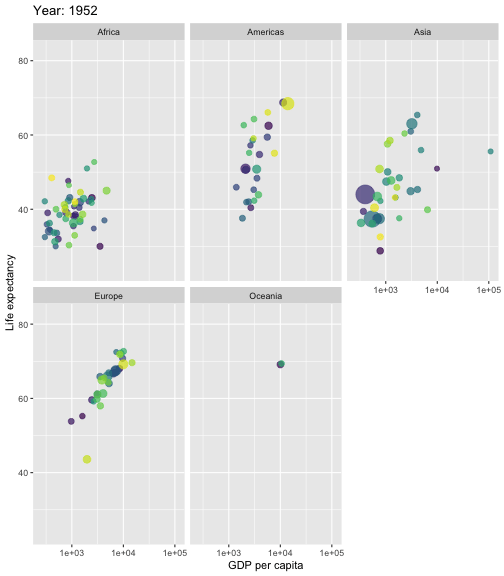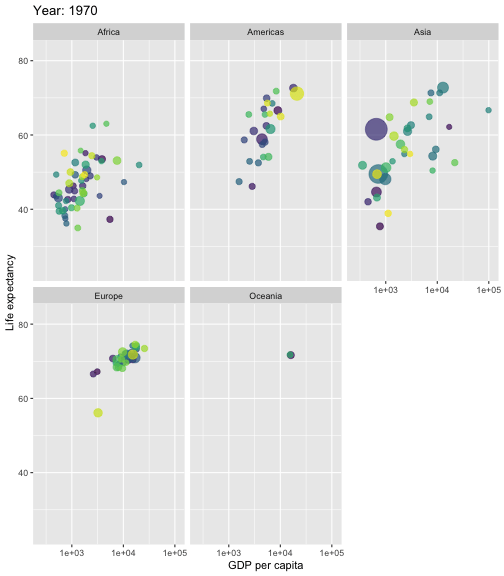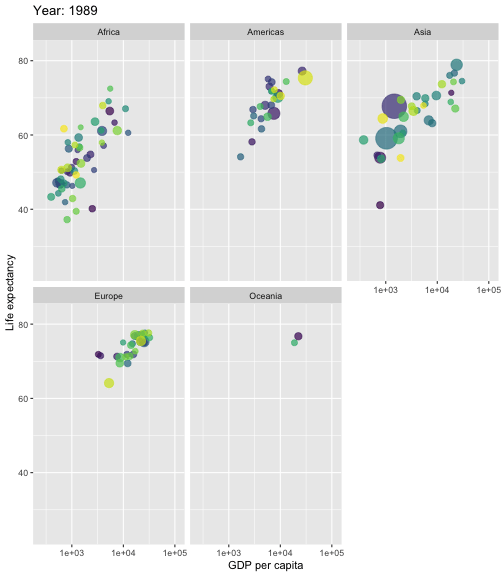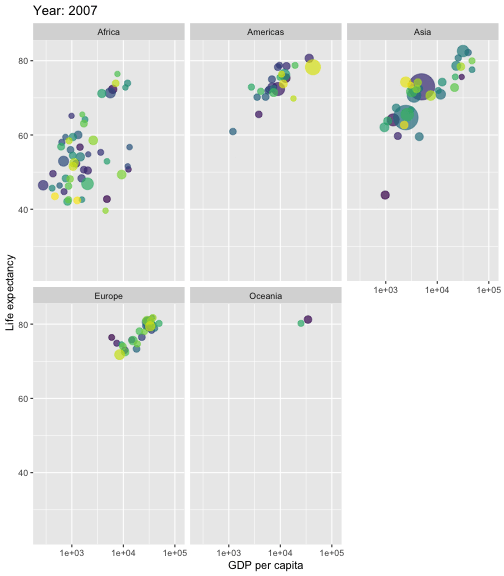
What is Regression Analysis?
- Statistical technique for investigating and modelling the relationship between variables.
Statistical Modelling
- a simplified, mathematically-formalized way to approximate reality (i.e. what generates your data) and optionally to make predictions from this approximation.
Statistical Modelling: The Bigger Picture
Software: R and RStudio (IDE) [Visit: https://hellor.netlify.app/]
Consider trying to answer the following kinds of questions:
- To use the parents’ heights to predict childrens’ heights.
mheight dheight1 59.7 55.12 58.2 56.53 60.6 56.04 60.7 56.85 61.8 56.06 55.5 57.9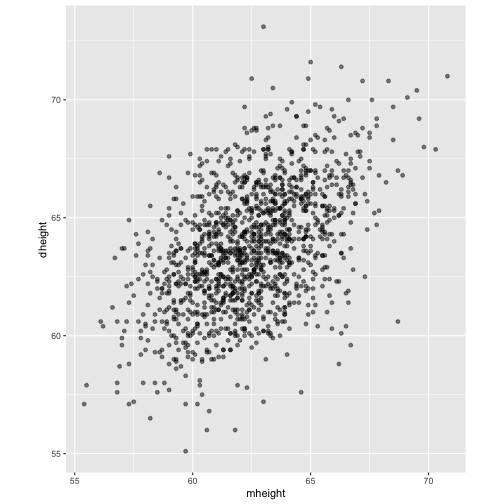
Predict the daughter's height if her mother's height is 66 inches?
Regression Analysis involves curve fitting.
Curve fitting: The process of finding a relation or equation of best fit.
Model
Y=f(x1,x2,x3)+ϵ
Goal: Estimate f ?
How do we estimate f?
Non-parametric methods:
estimate f using observed data without making explicit assumptions about the functional form of f.
Parametric methods
estimate f using observed data by making assumptions about the functional form of f.
Ex: Y=β0+β1x1+β2x2+β3x3+ϵ
Do not under-estimate the power of simple models.
Do not under-estimate the power of simple models.
- Create something new which is more efficient than the existing method.
Machine Learning Algorithms


Machine Learning Algorithms


Random Forest
XGboost
Neural networks, etc.
Pearson's Correlation Coefficient

Measures the strength of the linear relationship between two quantitative variables.
Does not completely characterize their relationship.
Pearson's Correlation Coefficient
cor(x,y)=∑Ni=1(xi−μx)(yi−μy)N∗σxσy
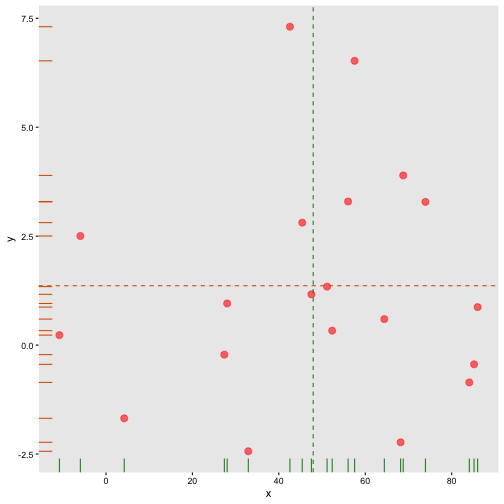
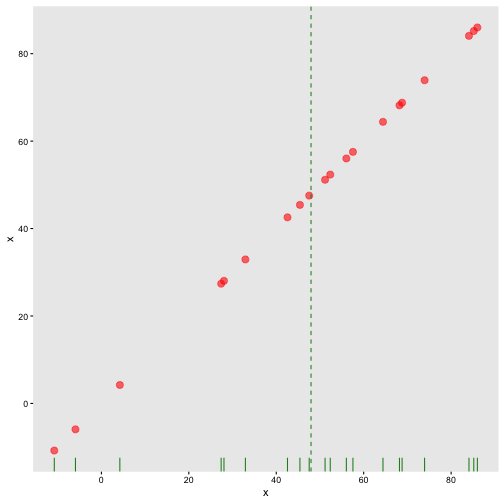
Covariance: Mean x
cov(x,y)=∑Ni=1(xi−μx)(yi−μy)N
Covariance: Mean y
cov(x,y)=∑Ni=1(xi−μx)(yi−μy)N
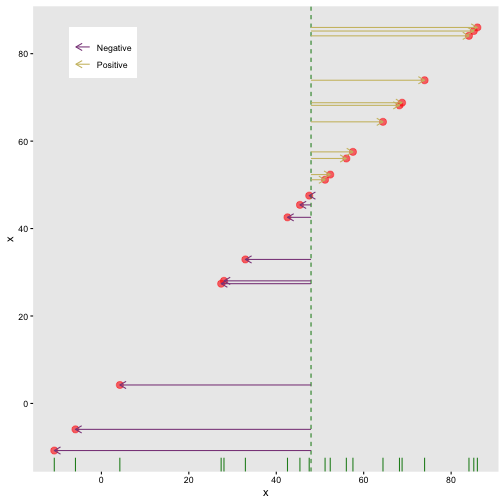
Covariance: differences x
cov(x,y)=∑Ni=1(xi−μx)(yi−μy)N
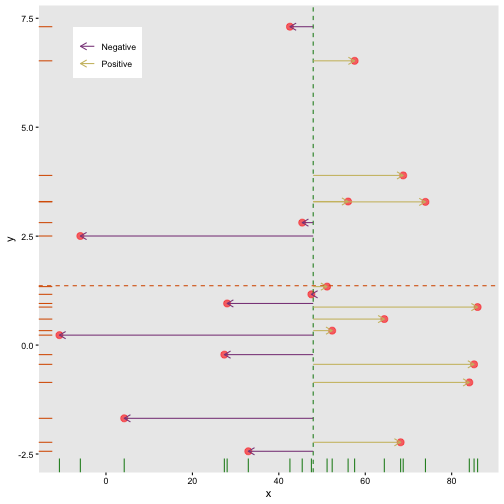
Covariance: Differences y
cov(x,y)=∑Ni=1(xi−μx)(yi−μy)N
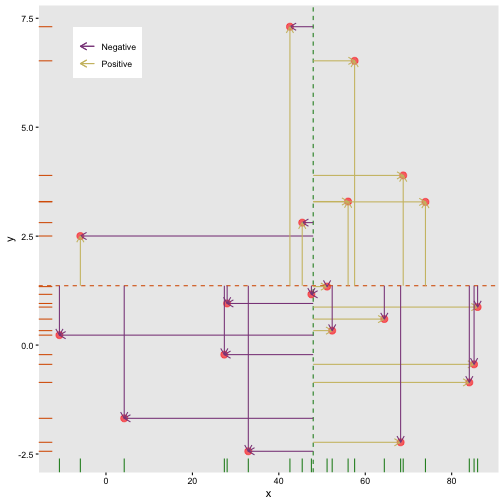
Covariance: Multiply differences
cov(x,y)=∑Ni=1(xi−μx)(yi−μy)N
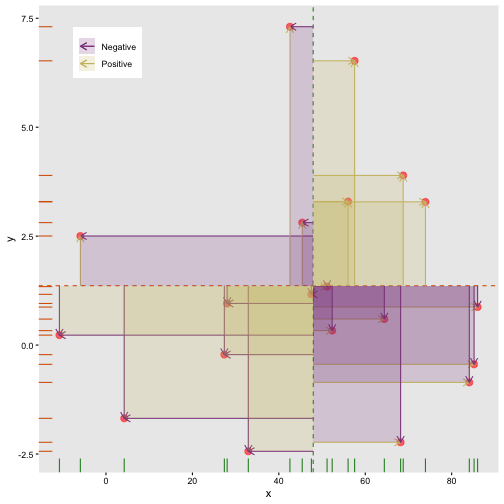
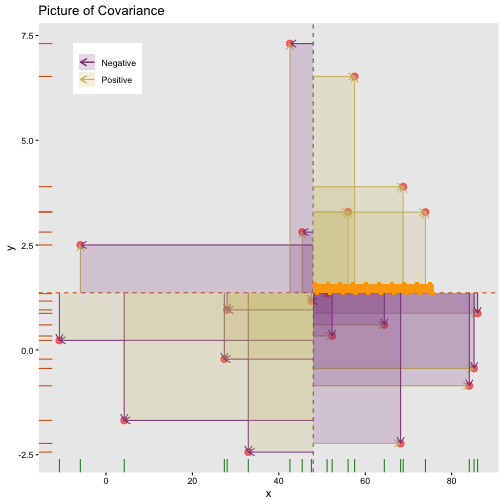
Covariance: take average rectangle
cov(x,y)=∑Ni=1(xi−μx)(yi−μy)N
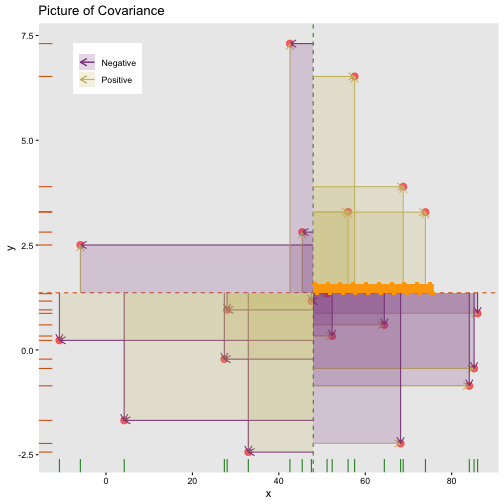
Covariance
cov(x,y)=∑Ni=1(xi−μx)(yi−μy)N
cor(x,y)=∑Ni=1(xi−μx)(yi−μy)N∗σxσy
cor(x,y)=cov(x,y)σxσy
Variance and Standard Deviations
σ2=∑Ni=1(xi−μx)2N
σ=√∑Ni=1(xi−μx)2N
Variance
σ2=∑Ni=1(xi−μx)2N
Variance
σ2=∑Ni=1(xi−μx)2N
Correlation: Beware
cor(x,y)=∑Ni=1(xi−μx)(yi−μy)N∗σxσy
cor(x,y)=∑ni=1(xi−¯x)(yi−¯y)(n−1)∗SxSy
Pearson's correlation coefficient
returns a value of between -1 and +1. A -1 means there is a strong negative correlation and +1 means that there is a strong positive correlation.
is very sensitive to outliers.
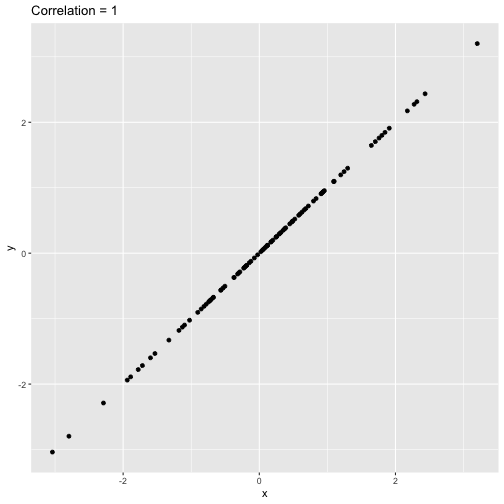
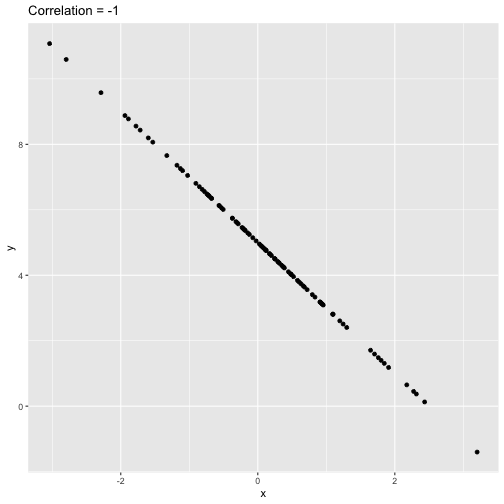
Pearson's correlation coefficient (cont.)
set.seed(2020)x <- rnorm(100)y <- rnorm(100)df <- data.frame(x=x, y=y)ggplot(df, aes(x=x, y=y)) + geom_point()+xlab("x") + ylab("y") + ggtitle("Correlation = -0.03") + coord_equal()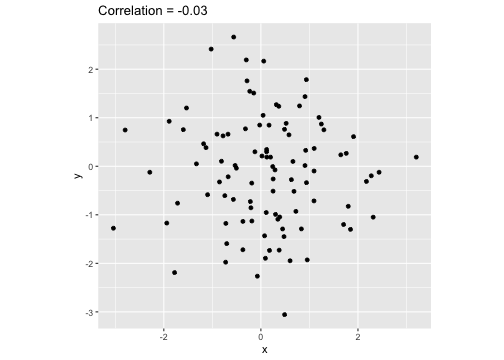
Pearson's correlation coefficient (cont.)
set.seed(2020)x <- seq(-2, 2, length.out = 20)y <- 5*x^2df <- data.frame(x=x, y=y)ggplot(df, aes(x=x, y=y)) + geom_point()+xlab("x") + ylab("y") + ggtitle("Correlation = ---")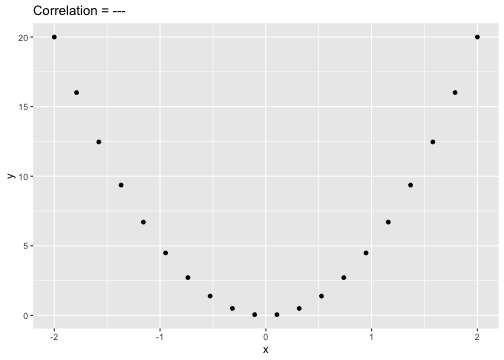
Pearson's correlation coefficient (cont.)
cor(x, y)[1] -1.70372e-16ggplot(df, aes(x=x, y=y)) + geom_point()+xlab("x") + ylab("y") + ggtitle("Correlation = 0.000")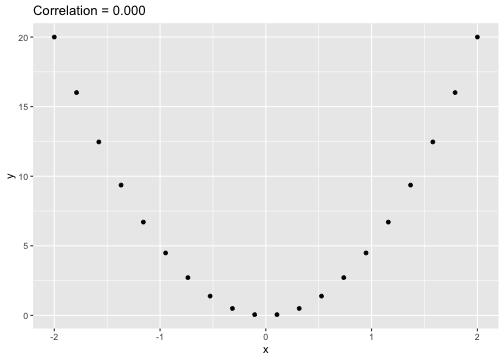
anscombe x1 x2 x3 x4 y1 y2 y3 y41 10 10 10 8 8.04 9.14 7.46 6.582 8 8 8 8 6.95 8.14 6.77 5.763 13 13 13 8 7.58 8.74 12.74 7.714 9 9 9 8 8.81 8.77 7.11 8.845 11 11 11 8 8.33 9.26 7.81 8.476 14 14 14 8 9.96 8.10 8.84 7.047 6 6 6 8 7.24 6.13 6.08 5.258 4 4 4 19 4.26 3.10 5.39 12.509 12 12 12 8 10.84 9.13 8.15 5.5610 7 7 7 8 4.82 7.26 6.42 7.9111 5 5 5 8 5.68 4.74 5.73 6.89x <- c(anscombe$x1, anscombe$x2, anscombe$x3, anscombe$x4)y <- c(anscombe$y1, anscombe$y2, anscombe$y2, anscombe$y4)z <- as.factor(rep(1:4, each=11))df <- data.frame(x=x, y=y, z=z)ggplot(df,aes(x=x,y=y,group=z))+geom_point(aes(col=z))+facet_wrap(~z)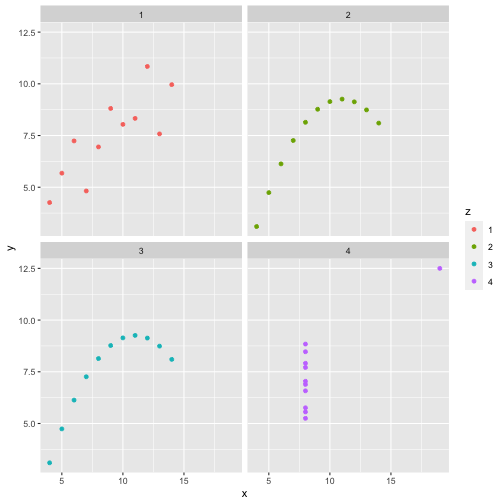
cor(anscombe$x1, anscombe$y1)[1] 0.8164205mean(anscombe$x1)[1] 9mean(anscombe$y1)[1] 7.500909cor(anscombe$x2, anscombe$y2)[1] 0.8162365mean(anscombe$x2)[1] 9mean(anscombe$y2)[1] 7.500909cor(anscombe$x3, anscombe$y3)[1] 0.8162867mean(anscombe$x3)[1] 9mean(anscombe$y3)[1] 7.5cor(anscombe$x4, anscombe$y4)[1] 0.8165214mean(anscombe$x4)[1] 9mean(anscombe$y4)[1] 7.500909Anscombe's quartet
x <- c(anscombe$x1, anscombe$x2, anscombe$x3, anscombe$x4)y <- c(anscombe$y1, anscombe$y2, anscombe$y2, anscombe$y4)z <- as.factor(rep(1:4, each=11))df <- data.frame(x=x, y=y, z=z)ggplot(df,aes(x=x,y=y,group=z))+geom_point(aes(col=z))+facet_wrap(~z)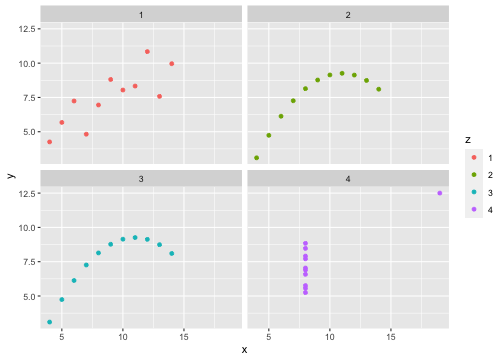
All four sets are identical when examined using simple summary statistics but vary considerably when grouped.
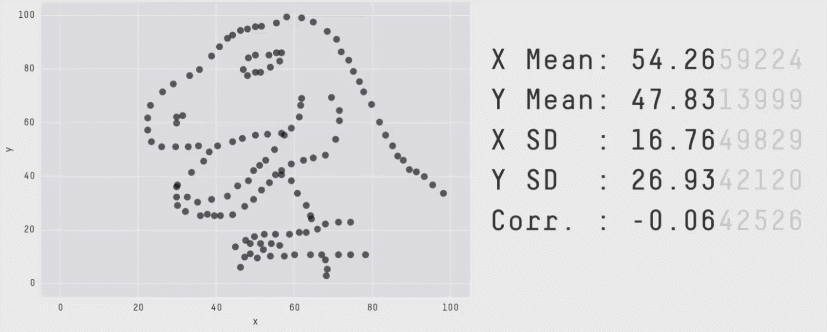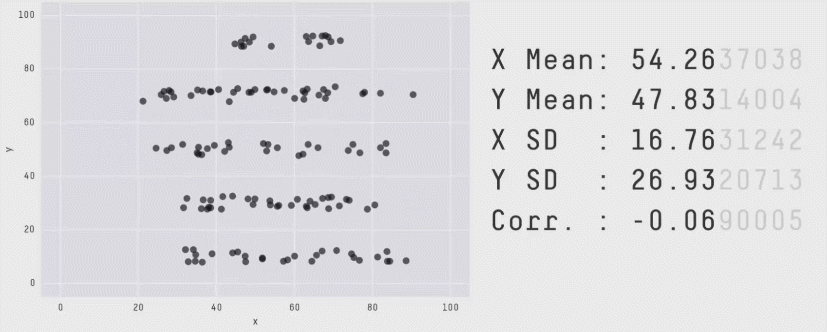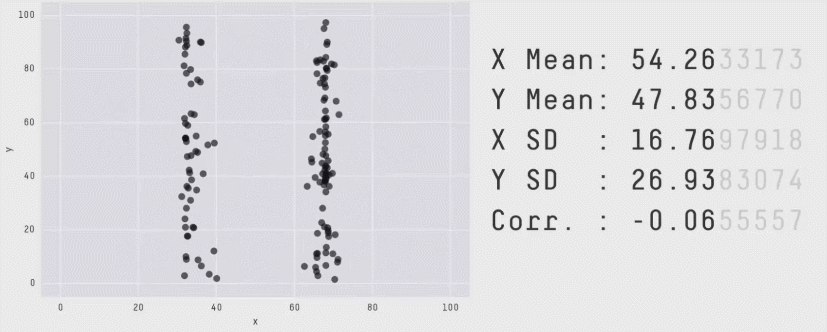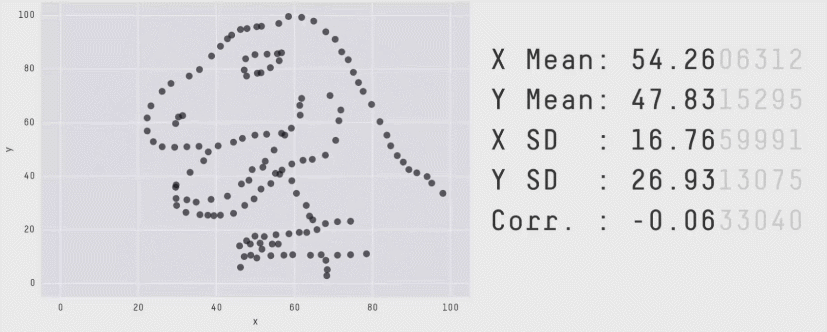
Acknowledgement: Justin Matejke and George Fitzmaurice, Autodesk Research, Canada
Regression Analysis
Functional relationship between two variables
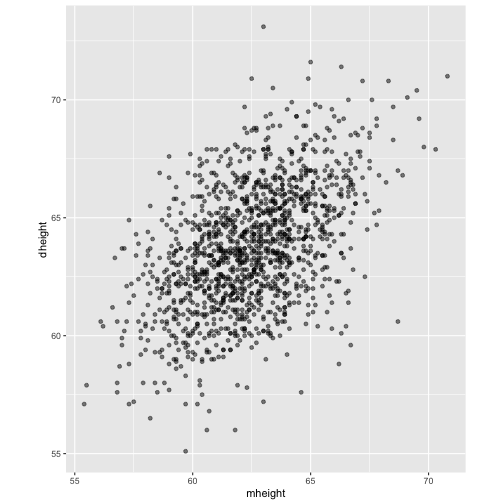
Functional relationship between two variables
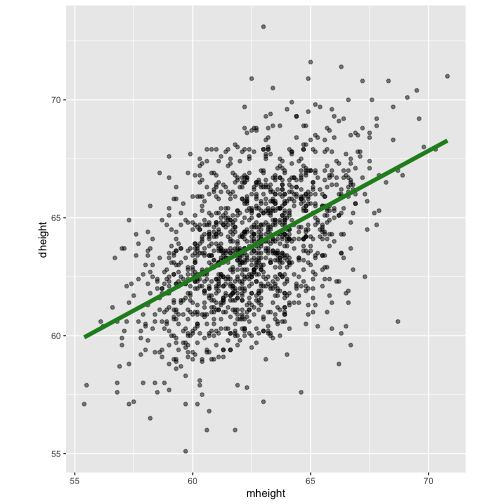
Functional relationship between two variables
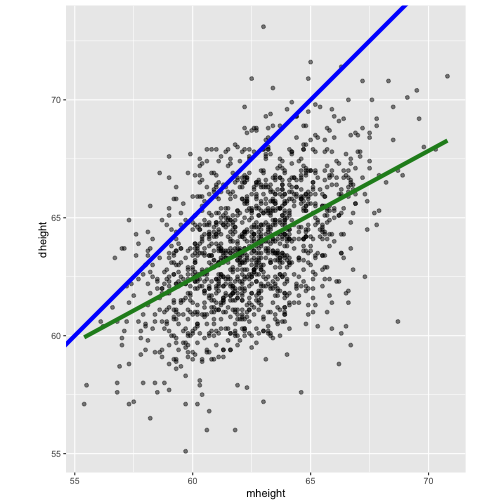
Functional relationship between two variables
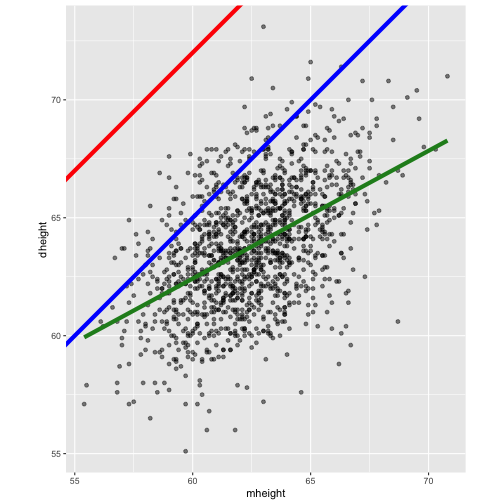
Simple Linear Regression
Simple - single regressor
Linear - regression parameters enter in a linear fashion.
Terminologies
Response variable: dependent variable
Explanatory variables: independent variables, predictors, regressor variables, features (in Machine Learning)
Parameter
Statistic
Estimator
Estimate
All rights reserved by
Acknowledgement
Gina Reynolds, University of Denver.